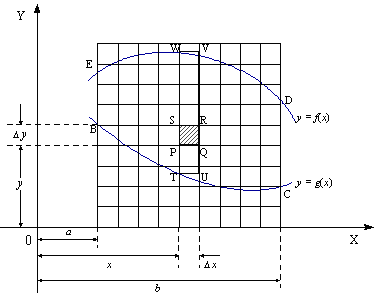
The Area as a Double Integral
Problem 1
Find the general formula as a double integral in
rectangular coordinates that allows to find the area between the lines
x = a, x = b and the curves y
= g(x), y = f(x).
Problem 2
Find the general formula as a double integral in rectangular
coordinates that allows to find the area between the lines y
= c, y = d and the curves x =
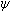 (y),
x =
(y),
x =  (y).
(y).
Problem 3
Find the general formula as a double integral in polar
coordinates that allows to find the area between the lines  =
=  ,
,  =
= 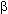 and the curves
r = g(
and the curves
r = g( ),
r = f(
),
r = f( ).
).

Problem 4
Find the general formula as a double integral in polar
coordinates that allows to find the area between the circles r
= a, r = b and the curves  =
= 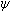 (r),
(r),
 =
=  (r).
(r).

Problem 5
The following graphics determine a series of curves
in polar coordinates and their general designation. Using the general
formulas of problems 4 or 5, find the area limited by the given
curves.








