The Volume as
a Triple Integral
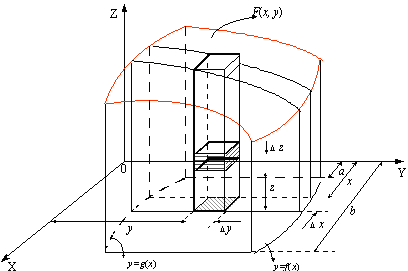
Problem 1
Find the general formula as a triple integral in rectangular
coordinates that allows to find the volume between the lines x
= a, x = b, the curves y = g(x),
y = f(x), and the surfaces z = 0, z
= F(x, y)
Problem 2
Using a triple integral in rectangular coordinates,
determine the volume of the solid in the first octant limited by the
surface z = 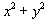 ,
and the planes y = x, x = 0, y
= 2, z = 0.
,
and the planes y = x, x = 0, y
= 2, z = 0.
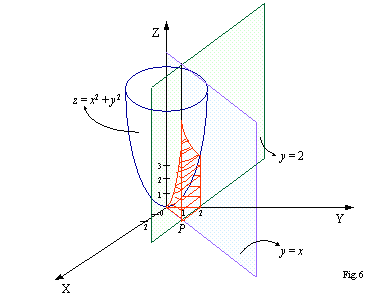
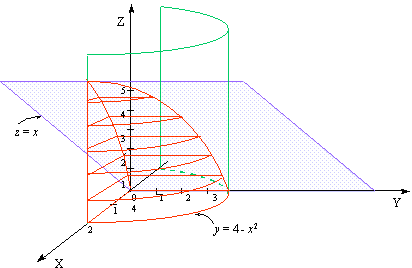
Problem 3
Using a triple integral in rectangular coordinates,
determine the volume of the solid in the first octant limited by the
cylinder
y = 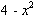 ,
and the planes z = x, y = 0, z =
0.
,
and the planes z = x, y = 0, z =
0.